The human circadian rhythm evolved as a mechanism by which living beings can synchronize their biological processes with the light and dark pattern of the terrestrial day. The circadian rhythm effectively functions as a master clock that regulates these processes. In humans, the circadian rhythm is tightly linked to various physiological processes, such as sleep, metabolism, and neuro-behavioral processes [1, 2].
Disruption of the circadian rhythm is known to have negative impacts on health, ranging from fatigue in travelers with jetlag to an increased risk of cardiac disease and cancer in rotating shift workers [3, 4]. Furthermore, malalignment of the circadian phase and related neurobehavioral states (such as alertness) with the timing of critical tasks may lead to lower performance and higher risk of failure.
The sleep process in humans is very tightly connected to the circadian rhythm. The sleep drive, for example, is known to be modulated by the circadian rhythm [5–7]. Sleep is critical to health, as it allows the body to recuperate and regenerate cells. It is also tied to neurocognitive performance; the lack of or mistiming of sleep have been empirically linked to degeneration of neurocognitive performance [8, 9] and disruption of circadian rhythm regulation [10, 11].
Many Department of Defense (DoD) missions necessarily disrupt natural circadian cycles and sleep. For example, airlift and tanker missions can impair reaction times, lower attention spans, diminish memory recall, and increase human errors and elevate risk [12]. Sleep duration is also found to affect cognitive performance [13]. Other research has shown that sleep cycle disruption may be more of a contributing cause than a symptom of PTSD experience in veterans [14]. Additionally, research conducted by the U.S. Naval Submarine Medical Research Laboratory, concludes that special operations forces may be able to phase-lock their circadian rhythms when traveling across time zones, via judicious control of light exposure [15].
In the circadian rhythm research literature, several mathematical models have been developed to capture the dynamics of circadian rhythm and sleep. These models are typically formulated to match experimental results from human subject studies. These models allow us to make quantitative predictions about, for example, the impact of lighting to a subject’s circadian rhythm, or the effects of circadian rhythm and sleep scheduling on a subject’s neurobehavioral states, such as alertness.
The models typically incorporate some parameters, such as the free-running period of the subject’s circadian rhythm, which may be adapted to individual subjects, leading to personalized circadian and sleep health solutions. In this article, we present a novel approach to mathematically modeling circadian rhythm and sleep activity and regulation.
Mathematical Modeling
Light is a strong synchronizer of the circadian rhythm. Generically, the circadian rhythm models are ordinary differential equations of the form
dx/dt = F(x,u), (1)
where x is the state of the circadian oscillator, and u represents the impact of light on the circadian oscillator. Because light can only attain non-negative intensity and its impact to the circadian oscillator has a saturation regime, u is typically constrained as:
0 ≤ u(t) ≤ umax , (2)
for all t ≥ 0.
These models come in various orders (i.e., levels of complexity). The highest order models could contain up to several dozens of state variables. These are typically based on the biochemical processes in the circadian gene regulation [16, 17]. Lower order models are typically empirical, such as the third order model by Kronauer et al. [18, 19], which uses a van der Pol oscillator to represent the circadian rhythm of core body temperature. A first order model is used to represent the dynamics of the phase of the circadian rhythm, which is a good approximation of the higher order dynamics under lighting conditions with low variation (e.g., a dark or dimly lit environment) [20].
The dynamics of the sleep and neurobehavioral states are coupled to that of the circadian rhythm. Their relationship is described in a family of models called the two-process models. These models link the dynamics of sleep drive and alertness to the circadian phase in a hybrid or multi-modal dynamical system:
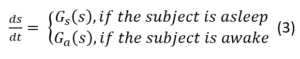
Here, s denotes the sleep and neurobehavioral states. Note that the dynamics of s(t) depends on whether the subject is asleep or awake. The transitions between the sleep and awake modes are determined by sleepiness. Sleepiness is quantified as variable B(t) and modeled as a function of the circadian and sleep states:
B(t) = H(x(t),s(t)). (4)
The switching between sleep and wakefulness can be modeled as spontaneous, with the subject going to sleep when sleepiness (B(t)) reaches a certain high level (Bmax) and waking-up when it reaches a certain low level (Bmin). An alternative approach is to assume that these switches can be scheduled in a constrained manner. For example, the subject can be scheduled to go to sleep when B(t) is between Bmax and BHmax and has to go to sleep when B(t) reaches BHmax for the schedule to avoid excessive sleep deprivation. Conversely, the subject can be scheduled to wake up when B(t) is between Bmin and BHmin and will wake up spontaneously when B(t) reaches BHmin. This is illustrated in Figure 1. The sleep state impacts the circadian state dynamics because the light stimuli cannot act on the subject while asleep.
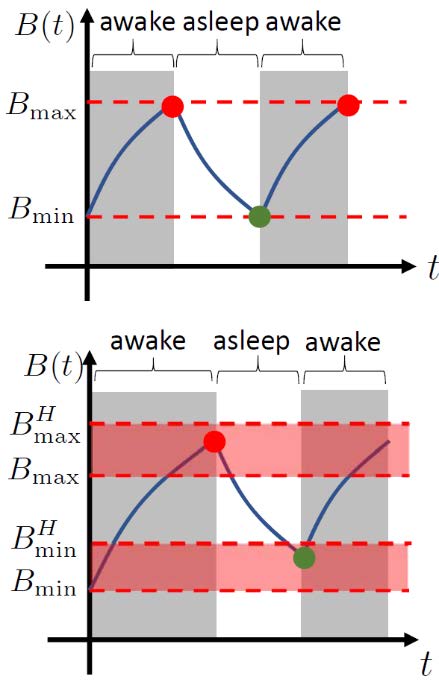
Figure 1. Illustrations of the spontaneous(top) and scheduled (bottom) sleep-wakeswitching. Red and green circles representthe times when the subject goes tosleep and wakes up, respectively.
Alertness, quantified as A(t), is modeled as a function of the sleep and neurobehavioral states [21–24]:
A(t) = K(x(t),s(t)). (5)
The factors that impact alertness in this model are sleep debt (whether the subject is lacking sleep), sleep inertia (whether the subject just recently gained wakefulness), and circadian phase (the subject’s biological clock).
Optimal Regulation of the Circadian and Sleep Process
Regulation of the circadian rhythm has been the subject of a great deal of research in recent years. From the perspective of biomathematics, this problem is typically expressed as an optimal control problem of a system with nonlinear dynamics. One of the main problems in optimal circadian rhythm regulation is the quickest entrainment problem, discussed below.
Quickest Entrainment Problem (QEP):
Given the dynamics of the circadian state in Equations (1–2), an initial condition x(0) = x0, and a reference circadian state trajectory xref(t), determine the input u(t) that minimizes the entrainment time T. Here, the entrainment time T is defined as the earliest time such that x(T) = xref(T).
The quickest entrainment problem can capture, for example, the problem of eliminating jetlag as quickly as possible. In this case, the reference xref(t) is the desired circadian state trajectory (without the jetlag).
QEP can be solved using optimal control techniques, resulting in both open-loop optimal lighting strategies [25, 26], where the optimal light signal is computed offline, and feedback optimal lighting strategies, where the optimal light signal is computed as a function of the current circadian state [20]. Note that the formulation of QEP ignores the dynamics of the sleep and neurobehavioral states (s(t)). Therefore, the resulting optimal solutions may be impractical from the sleep perspective, as they may require the subject to stay awake for an extended
period of time regardless of their sleepiness. To address this limitation, QEP can be modified to include the sleep dynamics. There are two variations of the new formulation, one where sleep is considered autonomous, and one where sleep can be scheduled, as discussed in the previous section.
Quickest Entrainment Problem with Autonomous Sleep (QEP-A):
Given the dynamics of the circadian, sleep, and neurobehavioral states in Equations (1–4), where the switching of the sleep dynamics is autonomous, an initial condition x(0) = x0, s(0) = s0, and a reference circadian state trajectory xref(t), determine the input u(t) that minimizes the entrainment time T. Here, the entrainment time T is defined as the earliest time such that x(T) = xref(T).
Quickest Entrainment Problem with Schedulable Sleep (QEP-S):
Given the dynamics of the circadian, sleep, and neurobehavioral states in Equations (1–4), an initial condition x(0) = x0, s(0) = s0, and a reference circadian state trajectory xref(t), determine the input u(t) and the sleep schedule that meets the scheduling constraint, such that the entrainment time T is minimized. Here, the entrainment time T is defined as the earliest time such that x(T) = xref(T).
QEP-A and QEP-S are more challenging to solve compared to QEP because the associated systems dynamics (a) have higher orders, and (b) is non-smooth because of the switching. Further, QEP-S is more challenging to solve compared to QEP-A due to the fact that QEP-S has more optimization variables and constraints (i.e., the sleep schedule).
Nevertheless, we recently developed a functional gradient descent method to solve these problems (samples of the solutions can be seen in Figure 2). The circadian rhythm model used to obtain these results are the third order Kronauer model [19]. The trajectories of the two circadian oscillator states and their respective references (with the subscript r) are shown in each graph. We can observe that, as expected, the solutions of QEP take the least amount of entrainment time compared to those of QEP-A and QEP-S. On the other hand, the solutions of QEP-A take the longest entrainment time because of the imposed constraint due to the autonomous sleep assumption.
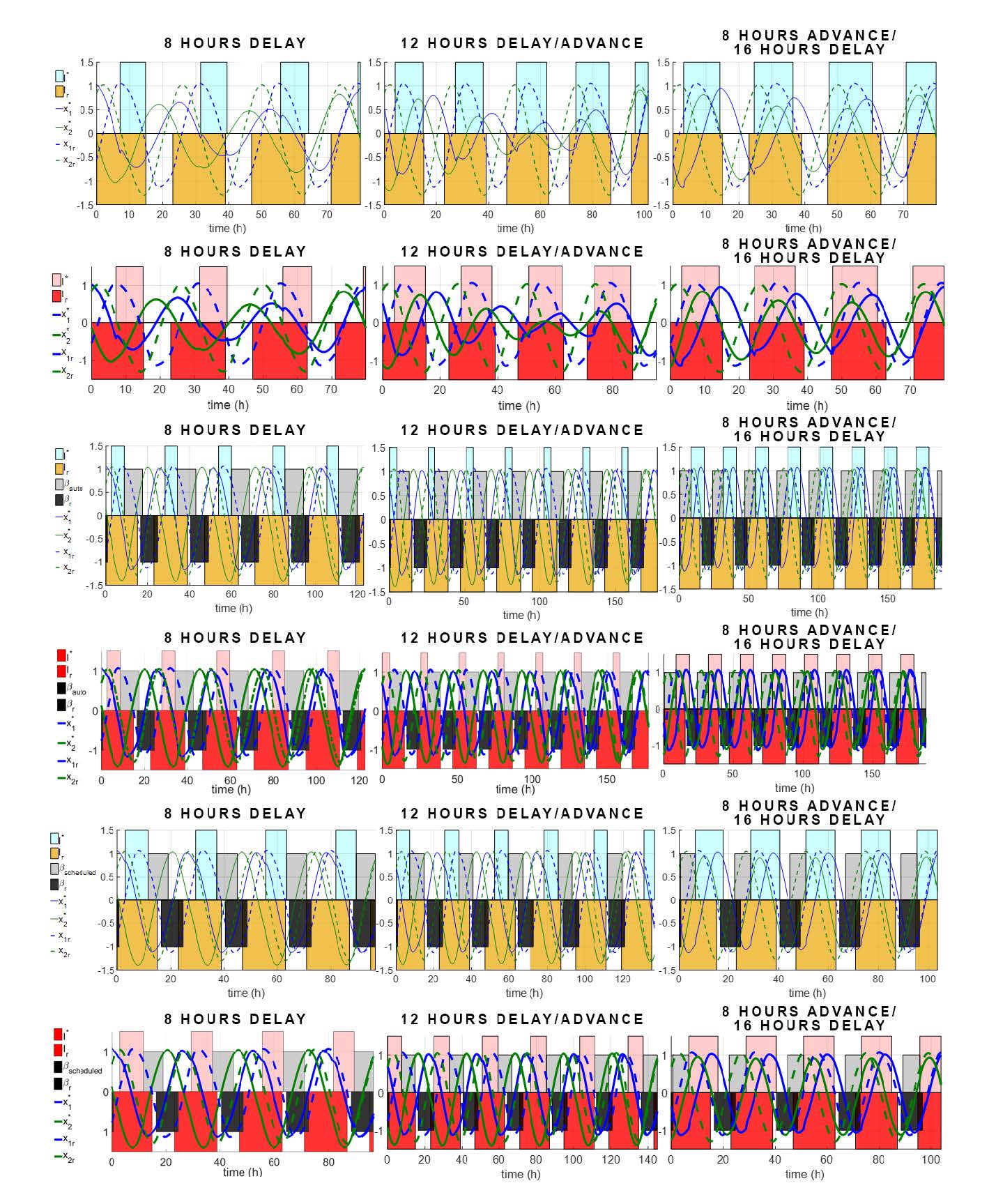
Figure 2. Solutions of QEP (top row), QEP-A (middle row), and QEP-S (bottom row), forvarious jetlag cases. All simulations are run until entrainment. Pink bands represent whenthe optimal control input (lighting) is on. Red bands represent when the natural (reference)daylight is on (assuming 16h/8h light/dark pattern). Light gray bands represent the sleepintervals of the subject. Dark gray bands represent the sleep intervals of the reference.
Another type of optimal control problems that can be formulated and solved for this system is the alertness optimization problem. The idea is to have the subject be maximally alert during a prescribed time interval, e.g., between given T1 and T2. Such a problem can be formulated as follows.
Alertness Optimization Problem (AOP):
Given the dynamics of the circadian, sleep, and neurobehavioral states in Equations (1–5), an initial condition x(0) = x0, s(0) = s0, determine the input u(t) and the sleep schedule that meets the scheduling constraint, such the minimum alertness Amin is maximized. Here, Amin
is defined as
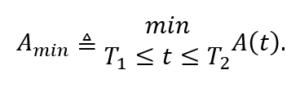
AOP can also be solved using a functional gradient descent method [27].
Table 1. Summary of papers that address the problems described in this article

┼ circadian dynamics refers to Eq. (1), sleep dynamics refers to Eq. (3)
* without the sleep scheduling constraints
Conclusion
Joint mathematical models for the circadian, sleep, and neurobehavioral processes are important tools for addressing problems related to the regulation of circadian rhythm, sleep, and optimization of alertness. These problems are related to practical DoD interests, such as the quick(est) elimination of jetlag and optimization of alertness in warfighters. Mathematically, they can be formulated as optimal control problems, for which there are solution techniques based on the calculus of variations.
Further research into circadian rhythm activity and sleep cycle regulation may help DoD maximize warfighter readiness and improve the force’s overall health and resilience to the rigors of military training and deployment.
Acknowledgements
The research in this article was supported by the National Science Foundation through the Smart Lighting Engineering Research Center (EEC-0812056) and in part by the U.S. Army Research Office through grant number W911NF-17-1-0562 and by New York State under NYSTAR contract C130145. The authors would like to thank Dr. Jiaxiang Zhang and Dr. Wei Qiao for their contributions to some of the results reported in this article, and Dr. Daniel Forger for valuable discussions related to optimal entrainment of circadian rhythms.
References
1. Smolensky, M. H., & Lamberg, L. (2001). The body clock guide to better health: How to use your body’s natural clock to fight illness and achieve maximum health. New York: H. Holt.
2. Foster, R. G., & Kreitzman, L. (2017). Circadian rhythms: A very short introduction. Oxford, United Kingdom: Oxford University Press.
3. Knutsson, A. (2003). Health disorders of shift workers. Occupational Medicine, 53(2), 103–108. doi:10.1093/occmed/kqg048
4. Figueiro, M. G., & White, R. D. (2013). Health consequences of shift work and implications for structural design. Journal of Perinatology, 33(S1). doi:10.1038/jp.2013.7
5. Borbély, A. A. (1982). A two process model of sleep regulation. Human Neurobiology, 1(3), 195–204.
6. Daan, S., Beersma, D. G., & Borbely, A. A. (1984). Timing of human sleep: Recovery process gated by a circadian pacemaker. American Journal of Physiology-Regulatory, Integrative and Comparative Physiology, 246(2). doi:10.1152/ajpregu.1984.246.2.r161
7. Achermann, P. (2004, March). The two-process model of sleep regulation revisited. Aviation, Space, and Environmental Medicine, 75(3), A37–A43.
8. Durmer, J. S., & Dinges, D. F. (2005). Neurocognitive consequences of sleep deprivation. Seminars in Neurology, 25(01), 117–129. doi:10.1055/s-2005-867080
9. Alhola, P., & Polo-Kantola, P. (2007). Sleep deprivation: Impact on cognitive performance. Neuropsychiatric Disease and Treatment, 3(5), 553–567.
10. Archer, S. N., Laing, E. E., Möller-Levet, C. S., Veen, D. R., Bucca, G., Lazar, A. S., . . . Dijk, D. (2014). Mistimed sleep disrupts circadian regulation of the human transcriptome. Proceedings of the National Academy of Sciences, 111(6). doi:10.1073/pnas.1316335111
11. Archer, S. N., & Oster, H. (2015). How sleep and wakefulness influence circadian rhythmicity: Effects of insufficient and mistimed sleep on the animal and human transcriptome. Journal of Sleep Research, 24(5), 476–493. doi:10.1111/jsr.12307
12. Criss, A G. (2018). Circadian rhythm disruption: A comparative analysis of enumeration for the mobility Air Force. Graduate Research Paper, Air Force Institute of Technology, Wright-Patterson AFB, Ohio. Retrieved from https://apps.dtic.mil/dtic/tr/fulltext/u2/1064133.pdf
13. Richards, A. (2017). When sleep isn’t perfect: Risk and resilience for cognitive consequences of imperfect sleep duration and suboptimal timing of tasks in circadian rhythm. U.S. Army Medical Research and Materiel Command (Report W81XWH-16-1-0259). Retrieved from https://apps.dtic.mil/dtic/tr/fulltext/u2/1057801.pdf
14. Kilgore, W. D. (2015). A nonpharmacologic method for enhancing sleep in PTSD. U.S. Army Medical Research and Materiel Command (Report W81XWH-14-1-0570). Retrieved from https://apps.dtic.mil/dtic/tr/fulltext/u2/1007313.pdf
15. Chabal, S., Couturier, K., Dyche, J., Soutiere, S., Figuiero, M., & Plitnick, B. (2018 January). Circadian rhythm phase locking for traveling special forces operators: Using light exposure to maintain time zone entrainment. Naval Submarine Medical Research Laboratory (Technical Report NSMRL/F1209/TR2018-1318). Retrieved from https://apps.dtic.mil/dtic/tr/fulltext/u2/1054520.pdf.
16. Leloup, J., & Goldbeter, A. (2003). Toward a detailed computational model for the mammalian circadian clock. Proceedings of the National Academy of Sciences, 100(12), 7051–7056. doi:10.1073/pnas.1132112100
17. Becker-Weimann, S., Wolf, J., Kramer, A., & Herzel, H. (2004). A model of the mammalian circadian oscillator including the EV-ERBα module. Genome Informatics, 15(4), 3–12. Retrieved from https://www.jstage.jst.go.jp/article/gi1990/15/1/15_1_3/_pdf
18. Kronauer, R. E., Forger, D. B., & Jewett, M. E. (2000). Quantifying human circadian pacemaker response to brief, extended, and repeated light stimuli over the phototopic range. Journal of Biological Rhythms, 14(6), 500–515.
19. Jewett, M. E., Forger, D. B., & Kronauer, R. E. (1999). Revised limit cycle oscillator model of human circadian pacemaker. Journal of Biological Rhythms, 14(6) 493–499.
20. Qiao, W., Wen, J. T., & Julius, A. A. (2017). Entrainment control of phase dynamics. IEEE Transactions on Automatic Control, 62(1), 445–450.
21. Achermann, P., & Borbely, A. A. (2003). Mathematical models of sleep regulation. Frontiers in Bioscience, 8, 683–693.
22. Jewett, M. E., & Kronauer, R. E. (1999). Interactive mathematical models of subjective alertness and cognitive throughput in humans. Journal of Biological Rhythms, 14(6), 588–597.
23. Rajdev, P., Thorsley, D., Rajaraman, S., Rupp, T. L., Wesensten, N. J., Balkin, T. J., & Reifman, J. (2013). A unified mathematical model to quantify performance impairment for both chronic sleep restriction and total sleep deprivation. Journal of Theoretical Biology, 331, 66–77. doi:10.1016/j.jtbi.2013.04.013
24. Ramakrishnan, S., Lu, W., Laxminarayan, S., Wesensten, N. J., Rupp, T. L., Balkin, T. J., & Reifman, J. (2015). Can a mathematical model predict an individual’s trait-like response to both total and partial sleep loss? Journal of Sleep Research, 24(3), 262–269. doi:10.1111/jsr.12272
25. Zhang, J., Qiao, W., Wen, J. T., & Julius, A. A. (2016). Light-based circadian rhythm control: Entrainment and optimization. Automatica, 68, 44–55. doi:10.1016/j.automatica.2016.01.052
26. K. Serkh and D. B. Forger, “Optimal schedules of light exposure for rapidly correcting circadian misalignment,” PLOS Computational Biology, 10(4), p. e1003523, 2014.
27. Serkh, K., & Forger, D. B. (2014). Optimal schedules of light exposure for rapidly correcting circadian misalignment. PLoS Computational Biology, 10(4). doi:10.1371/journal.pcbi.1003523
28. Zhang, J., Wen, J. T., & Julius, A. (2013). Optimal and feedback control for light-based circadian entrainment. 52nd IEEE Conference on Decision and Control. doi:10.1109/cdc.2013.6760287
29. Yin, J., Julius, A. A., & Wen, J. T. (2019, March). Rapid circadian entrainment in models of circadian genes regulation. arXiv:1902.09059. Retrieved from https://arxiv.org/pdf/1902.09059.pdf
30. Julius, A. A., Yin, J., & Wen, J. T. (2017). Time-optimal control for circadian entrainment for a model with circadian and sleep dynamics. 2017 IEEE 56th Annual Conference on Decision and Control (CDC). doi:10.1109/cdc.2017.8264355
31. Julius, A. A., Yin, J., & Wen, J. T. (n.d.). Optimization of light exposure and sleep schedule for circadian entrainment. Unpublished manuscript.


